This tool was created with the purpose of programming a vehicle to follow waypoints using an Arduino microcontroller paired to a GPS module.
To make editing easier, use the full-page view.
Creating and Loading Waypoints
- To create a waypoint path: click on the map.
- To remove a waypoint: click on the waypoint and click remove.
- To move a waypoint: click and drag it.
- To save or erase coordinates: right-click the map; the location name is the point of interest nearest to the first waypoint, and that is the file’s default name.
- To load coordinates from a file: right-click the map to load a JSON file and view the path on the map. The file must be an array of latitudes and longitudes as explained below.
- To add a vehicle: right-click the map and click place. A small bot will happily move around the waypoints with a simple algorithm at a fixed speed.
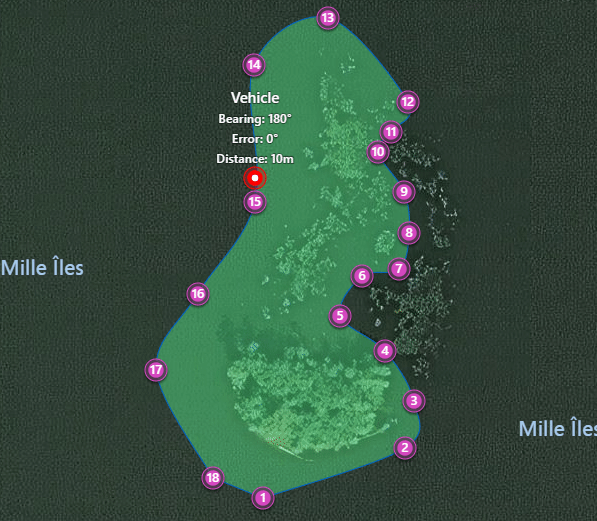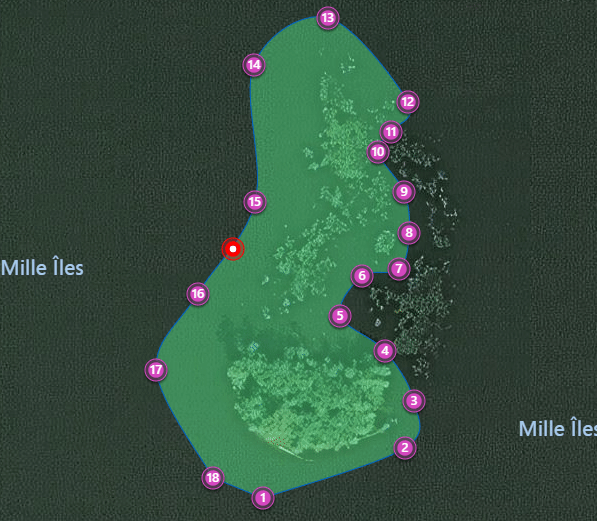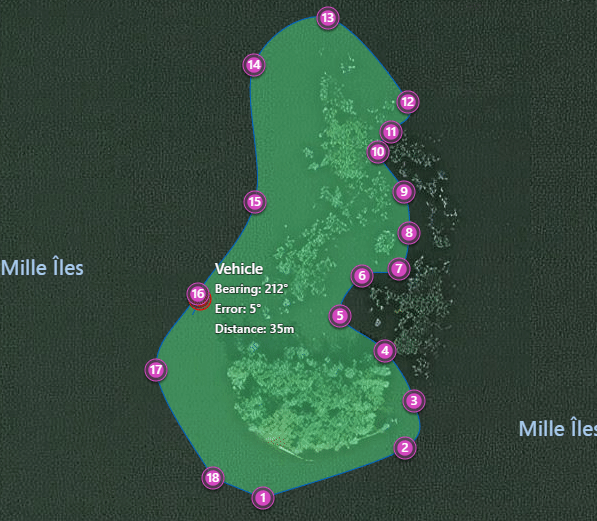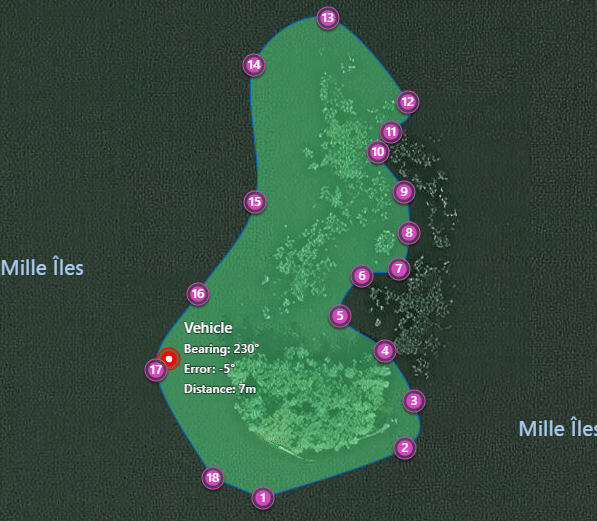
Output JSON
This map uses the Bing Maps API to add events that allow the user to create waypoints. The output file is a JSON array in the following format:
[{
"latitude": 45.66026005547925,
"longitude": -73.84635072708129,
"altitude": 0,
"altitudeReference": -1
},
{
...
}]
Each node in the array represents a waypoint, ordered from the first waypoint to the last. At the moment, only the latitude and longitude properties are used, the rest being complimentary information received from Pushpin.getLocation().
Problems Solved
In part for my future self, and in part to help others who need clear instructions as I do, here are a few solutions to geometric problems for directing an autonomous vehicle using geographic coordinates.
The simplest solution is to measure the vehicle’s heading angle compared to the target waypoint’s bearing angle, as explained below. This gives an angle off to the left or off to the right that the vehicle can correct for. This simulation uses a quack approximation to rotate the vehicle, but in real life the rudder of a boat or steering of a car would use a PID controller with a setpoint of 0 degrees (no error) and an input of the actual deviation off the target in degrees.
A better algorithm would include the concept of track – a line between the previous and next waypoints – and the vehicle’s distance from that track line would give the error. This would help protect from deviations caused by wind or current (a simple way to achieve this is to include more waypoints along the path).
How to Calculate Angle Between Two Geographic Coordinates
To predict whether a vehicle is heading in the right direction, one would need to find the angle between the vehicle and the target location. Is it really possible to calculate the angle between only two points? In fact, there is a third point: North. Technically, this is known as the bearing from one coordinate to the next.
For example, suppose a vehicle’s next waypoint is due North relative to the vehicle. In that case, the waypoint’s bearing relative to the vehicle is 0 degrees. If the waypoint were due East, its bearing to the vehicle would be 90 degrees. If it were due South, 180 degrees, and so forth.
Code below is inspired from an answer on Stack Overflow: Calculate angle between two Latitude/Longitude points. Because coordinates in degrees must be converted to radians, a little function locationToRadians() converts a location {latitude, longitude} to radians.
// Find the bearing between two coordinates.
function bearingBetweenCoordinates(location1, location2) {
location1 = locationToRadians(location1)
location2 = locationToRadians(location2)
let longitudeDifference = location2.longitude - location1.longitude
let y = Math.sin(longitudeDifference) * Math.cos(location2.latitude)
let x = Math.cos(location1.latitude) * Math.sin(location2.latitude)
- Math.sin(location1.latitude) * Math.cos(location2.latitude)
* Math.cos(longitudeDifference)
let bearing = Math.atan2(y, x)
bearing = radiansToDegrees(bearing)
bearing = (bearing + 360) % 360
return bearing
}
// Convert a location in degrees to a location in radians.
function locationToRadians(location) {
return {latitude: degreesToRadians(location.latitude),
longitude: degreesToRadians(location.longitude)}
}
// Convert degrees to radians.
function degreesToRadians(degrees) {
return degrees * (Math.PI / 180)
}
How to Calculate Angle Between Vehicle Direction and its Target Location
When traveling with a vehicle to a waypoint, one would like to know whether the vehicle’s direction is correct. A simple way to do this is to draw a line ahead of the vehicle: this is the vehicle’s heading. Heading is calculated in degrees away from North, where 90.0 is East, 180.0 is South, etc. The location the vehicle wants to reach also has an angle: the bearing from the vehicle to that point.
To find how far away the vehicle is pointing, simply subtract heading from bearing. That is, if the vehicle is heading 30 degrees North, and the target location’s bearing is 30 degrees, then 30.0 - 30.0 == 0, meaning that the vehicle is heading straight on target.
If the vehicle were heading 25 degrees North, but the target’s bearing is still 30 degrees, then heading - bearing == 25.0 - 30.0 == -5.0. The vehicle is pointing -5 degrees to the target’s left. If the result were +5 degrees, the vehicle would be pointing to the target’s right.
The code to find this heading error is shown below, as inspired from a snippet on Stack Overflow:
// Find how many degrees right or left one heading is to the next.
// Left degrees are negative and right degrees are positive.
// Always returns the shortest angle.
function headingError(bearing, heading) {
// Get both angles; these add to 360 degrees, but one is smaller
let leftAngle = bearing - heading
let rightAngle = heading - bearing
// Make non-negative
if(leftAngle < 0)
leftAngle += 360
if(rightAngle < 0)
rightAngle += 360
// Return the most acute angle, and make leftwards angles negative
return leftAngle < rightAngle ? -leftAngle : rightAngle
}
The code above corrects for situations where a simple subtraction does not give the ideal answer. For example, what happens if heading = 350.0 and bearing = 10.0? Is the vehicle pointing 340 degrees to the waypoint’s right?
Calculating Distance between Two Locations on Earth
To know whether a vehicle has arrived at a waypoint requires measuring distance. One might also want to know other distance information, like the path’s total length.
Accurately finding two distances on earth requires including the earth’s sphericity. To test this function’s accuracy, try inputting two cities with a known distance between them.
Of course, for our purposes, one could assume the earth is flat, but this is more fun. Code shamelessly taken from Calculate distance between 2 GPS coordinates on Stack Overflow:
// Find distance between two locations in meters.
function distanceInMetersOnEarth(location1, location2) {
let earthRadiusM = 6371000;
let dLat = degreesToRadians(location2.latitude - location1.latitude);
let dLon = degreesToRadians(location2.longitude - location1.longitude);
let lat1 = degreesToRadians(location1.latitude);
let lat2 = degreesToRadians(location2.latitude);
let a = Math.sin(dLat/2) * Math.sin(dLat/2) + Math.sin(dLon/2)
* Math.sin(dLon/2) * Math.cos(lat1) * Math.cos(lat2);
let c = 2 * Math.atan2(Math.sqrt(a), Math.sqrt(1-a));
return earthRadiusM * c;
}
Projecting a Point from a Location at a Certain Angle
To show the vehicle’s projected path, one must project a point before the vehicle based on its current heading. Solution from Calculate point, given x, y, angle, and distance on Stack Overflow. Keep in mind that the input location here is an object in the format {latitude, longitude}.
// Project a point from a certain location at a certain angle.
// Returns the other point needed to complete this line.
// https://math.stackexchange.com/a/143946/769532
// x = distance * cos(θ), y = distance * sin(θ)
function projectPoint(location, angle, distance) {
distance = distance * .00001 // This factor needs adjustment
angle = degreesToRadians(angle)
let latitude = location.latitude + (distance * Math.cos(angle))
let longitude = location.longitude + (distance * Math.sin(angle))
return {"latitude": latitude, "longitude": longitude}
}
This function may be slightly inaccurate because it assumes the earth is flat, but it is sufficient for our needs. In this way, one would use a GPS module to track the vehicle’s location, and a compass for the vehicle’s current heading. Those two inputs are sufficient to project a point from the vehicle’s location at the heading’s angle an arbitrary distance away (or using a vector of a certain length to reflect speed). A line can then be drawn from the vehicle’s location to the projected point.